Descubriendo la regresión logística - Koldo Pina - Data Science & Inteligencia Artificial

La regresión logística se utiliza para resolver problemas de clasificación. Consiste en obtener una estimación de probabilidades para variables de respuesta categóricas. La suma de las probabilidades de cada variable de respuesta será igual a uno.

Para hacerlo más sencillo, nosotros vamos a considerar únicamente dos categorías posibles, cero y uno, para la variable respuesta estimada para un suceso. Tenemos entonces que la variable respuesta será:

$y_{i} = \begin{cases} 0 & P_{i}(0) = 1-p_{i}\\ 1 & P_{i}(1) = p_{i} \end{cases}$

donde la probabilidad de pertenecer a la categoría uno para cada evento es p_i.

Para construir una regresión logística, se parte de la expresión para la regresión lineal simple, que tiene esta pinta:

$\begin{matrix} f(x) = y = a + b \cdot x & Dominio = \mathbb{R}\\ & Imagen =\mathbb{R} \end{matrix}$

Ésta función tiene como dominio y como imagen a todos los números reales. Luego los valores de la variable respuesta serán continuos.

Ahora imaginemos que queremos predecir con estos dos modelos la probabilidad de que un evento ocurra, la cual se encuentra en el rango entre cero y uno.

Una gráfica que ilustra el comportamiento de los modelos podría ser ésta:

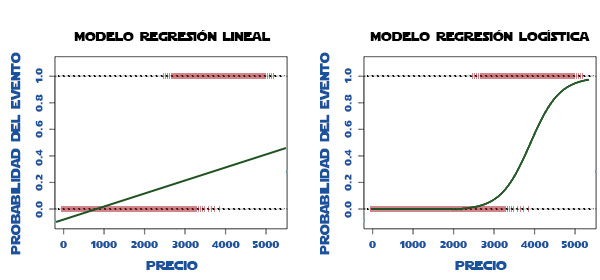
Figura 1

En ella podemos ver los dos modelos de regresión, el lineal y el logístico, prediciendo la probabilidad de que suceda dicho evento, la cual depende del precio de un ítem. Como se ve en la gráfica para el modelo de regresión lineal, nos encontramos con el problema de que para precios entre 0 y 500, la probabilidad del evento es negativa. También nos podría ocurrir que la recta de regresión lineal tomara valores por encima de uno para valores de precio muy elevados. Sin embargo, el modelo de regresión logística mantiene entre cero y uno los posibles valores de la probabilidad de que ocurra el evento, y esto es lo que nos va a interesa para hacer una buena clasificación.

Así que nuestro objetivo va a ser conseguir una función que modele la probabilidad de que y pertenezca a una de las dos categorías, cero o uno, partiendo de la ecuación para la regresión lineal.

Teniendo esto en cuenta, el rango de nuestra función objetivo deberá estar entre 0 y 1.

Para ello tendremos que hacer algunas transformaciones sobre la función de la regresión lineal, y utilizar el concepto de Odds del que hablé en este post.

Según esto, podemos hacer nuestro primer movimiento, igualando la ecuación de regresión lineal a una probabilidad:

$P = a + b \cdot x$

Ésta probabilidad será la probabilidad condicionada de que un evento pertenezca a la categoría cero o a la categoría uno, dadas unas variables de entrada X. En notación matemática se escribiría así, por ejemplo, para y = 1:

$P(x) = P (y = 1 | x)$

y su rango está entre cero y uno.

Pero nosotros necesitamos un rango como el de la regresión lineal, esto es, todo R, para que el rango sea el mismo a los dos lados de la igualdad.

Nuestro siguiente paso puede ser decir, bueno, en vez de usar la probabilidad, podemos usar el Odds, del que conocemos su rango, [0, ∞), con lo que tendríamos:

$\frac{p}{1-p} = a + b \cdot x$

Bien. Nos vamos acercando a nuestro objetivo de que el rango sea todo R.

Lo tenemos a huevo. Si aplicamos el logaritmo neperiano al Odds, su rango pasará a ser (-∞ , ∞):

$\ln\begin{pmatrix}\frac{p}{1-p}\end{pmatrix}= a + b \cdot x$

Y ya tenemos que a ambos lados de la igualdad, las funciones tienen el mismo rango, R.

Por cierto, a la expresión

$\ln\begin{pmatrix}\frac{p}{1-p}\end{pmatrix}$

se la llama función logit.

Ahora solo nos faltaría despejar p, siguiendo estos pasos:

$e ^{\ln\begin{pmatrix}\frac{p}{1-p}\end{pmatrix}} = e^{a + b \cdot x} \Rightarrow$

$\frac{p}{1-p} = e^{a \cdot x + b} \Rightarrow p = (1-p) \cdot e^{a + b \cdot x}$

$p = e^{a + b \cdot x} - e^{a + b \cdot x} \cdot p \Rightarrow$

$p + e^{a + b \cdot x} \cdot p = e^{a + b \cdot x} \Rightarrow$

$p \cdot (1 + e^{a + b \cdot x}) = e^{a + b \cdot x} \Rightarrow$

$p = \frac{e^{a + b \cdot x}}{1 + e^{a + b \cdot x}}\Rightarrow$

$p = \frac{\frac{e^{a + b \cdot x}}{e^{a + b \cdot x}}}{\frac{1}{e^{a + b \cdot x}} + \frac{e^{a + b \cdot x}}{e^{a + b \cdot x}}}\Rightarrow$

$\boxed{p = \frac{1}{1 + e^{-(a + b \cdot x)}}}$

La función que hemos obtenido, se llama función sigmoide, y su expresión más general se puede escribir así:

$\boxed{y = \frac{1}{1 + e^{-f(x)}}}$

donde

$\begin{array}{rcr} f(x) = a + b \cdot x & para\hspace{4}la\hspace{4}regresi\acute{o}n\hspace{4}lineal\hspace{4}simple \\ f(x) = a + \sum_{i=1}^{n} b_{n} \cdot x_{n} = a + \vec{B} \cdot \vec{X} & para\hspace{4}la\hspace{4}regresi\acute{o}n\hspace{4}lineal\hspace{4}m\acute{u}ltiple$

Haciendo una sencilla función en Python podemos ver su gráfica:

import numpy as np
import matplotlib.pyplot as plt

def sigmoide(x):
    res = [1 / (1 + np.exp(-ele)) for ele in x]
    return res

x = np.arange(-15, 15, 0.5)
y = sigmoide(x)
y_mid = [0.5 for ele in x]

fig = plt.figure()
sg = fig.add_subplot(111)

sg.set_title('función sigmoide',fontsize=16, fontweight='bold')

sg.set_xlabel('x')
sg.set_ylabel('y')

sg.text(-7, 0.9, r'', style='italic',fontsize=15,
        bbox={'facecolor': 'green', 'alpha': 0.3, 'pad': 10})

sg.text(-15, 0.53, r'pto inflexión: y=0.5', fontsize=15, color='red')

plt.plot(x, y, color='#1F5320', lw = 3.0)
plt.plot(x, y_mid, color='red', lw = 2.0, ls = 'dashed')

plt.show()

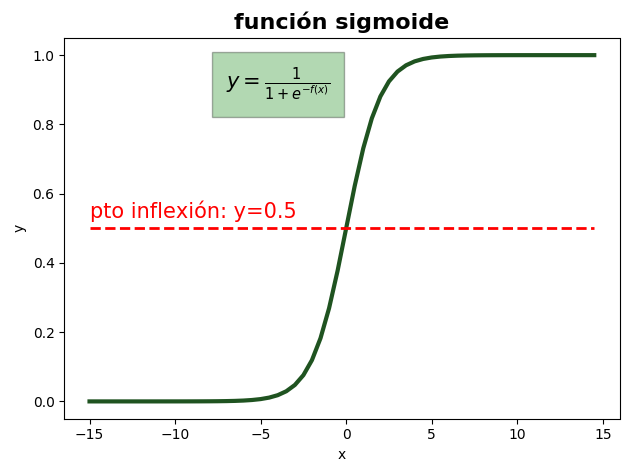
Función sigmoide

Quedarían dos cosas importantes por hacer:

La función que hemos calculado devuelve una estimación de una probabilidad. Para poder utilizarla como clasificador, hay que definir un límite (threshold). En función de si el valor devuelto por la función es mayor o menor que ese límite, clasificaremos el evento. Por ejemplo, en la gráfica he puesto en rojo la línea de probabilidad igual a 0.5, que podría utilizarse como límite. Para valores superiores, el evento pertenecería a una clase, y para valores menores o iguales, a otra. Sin embargo, este límite debe ser fijado sabiamente, teniendo en cuenta las características del problema a resolver.
Para poder utilizar este modelo, debemos calcular los coeficientes de la ecuación de regresión lineal. Para ello se aplica el método de máxima verosimilitud. Lo veremos en un siguiente post.

Puedes descargarte el código de mi

Never Tell Me The Odds!

I'm your maximum likelihood estimate

También puede gustarte

Cómo no caer en la Fosa de Carkoon. El equilibrio entre la varianza y el sesgo.

Más agrupaciones de datos en Python…sin Pandas

Your Empire needs you! Y también a la regresión logística.

Deja una respuesta Cancelar la respuesta