A la hora de elegir un método de aprendizaje estadístico tenemos que tener en cuenta un concepto importante: el equilibrio entre la varianza y el sesgo.

El sesgo es el error que introducimos en el modelo, al intentar explicar un problema del mundo real, al que le correspondería un modelo muy complicado, con un modelo bastante más simple. Podríamos pensar en el sesgo como en el cuánto generalizamos nuestro modelo. En general, modelos más flexibles, menos generalizados y más complejos, implican menos sesgo. El sesgo, entonces, no es consecuencia de nuestros datos, sino del modelo elegido.

Y la varianza es la cantidad en la que cambiaría mi predicción si la estimáramos con un conjunto de datos diferente.  Por ejemplo, un modelo que se ajuste mucho a unos datos sufrirá una varianza considerable al cambiar dichos datos, y viceversa. En general, modelos más flexibles, menos generalizados y más complejos, implican una mayor varianza.

Podemos concluir entonces que, cuanto más flexible sea nuestro modelo, la varianza aumentará, y el sesgo disminuirá.

Por lo tanto, debemos fijarnos en estos dos amigos, ya que pueden introducir en nuestro modelo un montón de ruido y, por tanto, hacerlo menos preciso. Con un análisis de ambos podemos evaluar el rendimiento de nuestro modelo.

Una buena gráfica donde se observa el efecto del sesgo y la varianza sobre la precisión de la predicción de un modelo es esta, donde los puntos sobre la diana son diferentes ejecuciones de nuestro modelo.

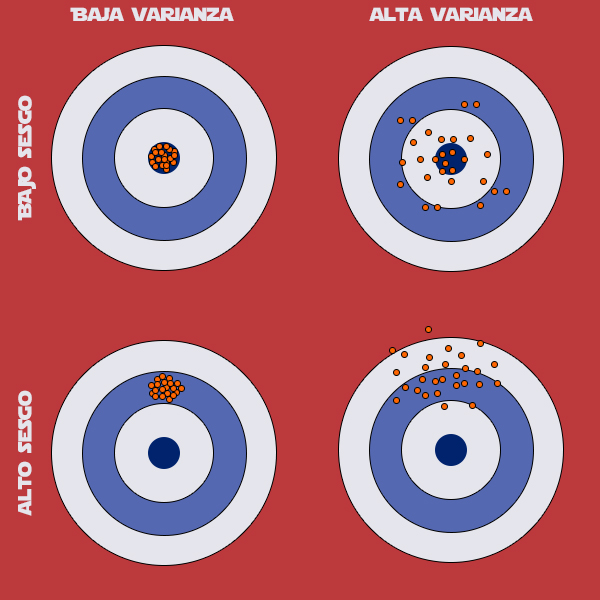
Pero, ¿qué significa que un modelo sea flexible? Flexibilidad es sinónimo de complejidad. Cuanto más cercano es el modelo a los datos de entrenamiento, más flexible es, y viceversa. El aumento de la flexibilidad conlleva un aumento de la complejidad del modelo, lo que disminuye su interpretabilidad y aumenta la posibilidad de caer en el sobreajuste (overfitting) del modelo, disminuyendo el sesgo, lo que también disminuiría considerablemente la precisión de la predicción.

Un ejemplo de un modelo poco flexible sería la regresión lineal. Y uno muy flexible podría ser máquinas de vector soporte.

Podemos ver una gráfica que relaciona la flexibilidad con la interpretabilidad de varios tipos de modelos.

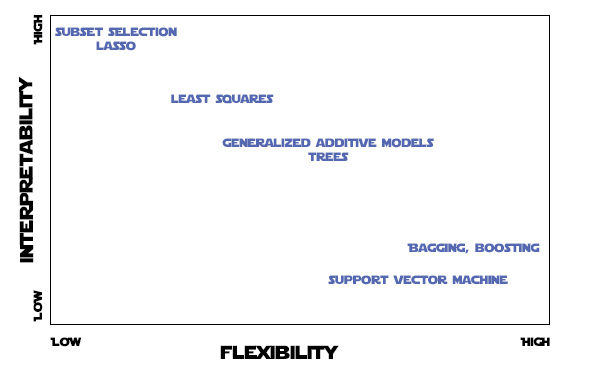
A veces, partiendo de un modelo sencillo de regresión lineal, puedes acabar con un modelo más complicado al querer reducir el error en la predicción. Lo que resulta es que el modelo se ajustará a todos los puntos de un conjunto de datos. El problema con este modelo tan complejo, es que se ha ajustado tanto a unos datos, que no podrá predecir basándose en nuevos datos que no estén en la curva del modelo.

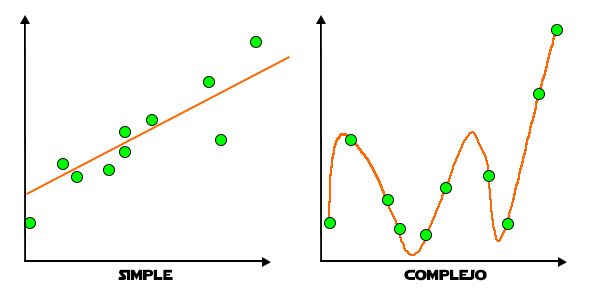
Vamos a ver con tres gráficas este efecto del aumento de la complejidad del modelo sobre el error en la predicción.

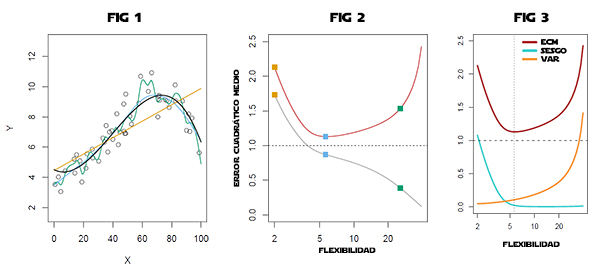
En la figura 1 se representan varios modelos. La curva en negro es el modelo real que siguen los datos. Los puntos son ruido. La curva en amarillo, es un modelo de regresión lineal. Y las curvas en azul y en verde son modelos más complejos de ajuste lineal.

En la figura 2, está representada la flexibilidad del modelo frente al error cuadrático medio. La línea gris corresponde a los datos de entrenamiento y la línea roja corresponde a los datos de test. Podemos ver que los errores siguen la misma tendencia tanto en entrenamiento, como en test, a flexibilidad (o complejidad) baja del modelo. Sin embargo, al aumentar la complejidad vemos que, aunque el error en los datos de entrenamiento disminuye, el error en los datos de test se dispara.

En la figura 3 se representa el error, el sesgo y la varianza frente a la flexibilidad. La línea vertical de puntos indica el menor valor del error para los datos de test, que también sería el punto de complejidad optima del modelo.

Parece claro entonces que el objetivo consiste en conseguir un modelo en el que tanto la varianza como el sesgo sean lo más bajos posible, ya que así aumentará la precisión de nuestra predicción, encontrando un equilibrio entre ellos.

Entonces, parece muy importante tener en cuenta estos conceptos a la hora de desarrollar un modelo de aprendizaje estadístico. ¿Existe algún método para evitar entrar en zonas no deseadas? Si. Por ejemplo, como acabamos de ver en la gráfica anterior, separar el conjunto de datos del que disponemos, en dos subconjuntos. Un conjunto sería el que utilizaríamos para entrenar el modelo (conjunto de entrenamiento) y otro conjunto sería el utilizado para el cálculo del error del modelo (conjunto de prueba).  Los datos se deben dividir de manera aleatoria, tomando por ejemplo un 70% de los mismo para el conjunto de entrenamiento y el 30% restante para el conjunto de prueba.

El siguiente gráfico representa muy bien esta idea:

En el gráfico, si nos movemos de izquierda a derecha, va aumentando la complejidad de nuestro modelo. A su vez, baja el sesgo y aumenta la varianza. De tal manera que el error en los datos de entrenamiento y en los datos de test tiene la misma tendencia, hasta que llega un momento en el que el error en los datos de test empieza a aumentar mientras que el de entrenamiento sigue disminuyendo. Ese punto mínimo de error en los datos de test nos indica el nivel de complejidad óptimo para nuestro modelo. Si seguimos modificando nuestro modelo para hacerlo más flexible, aumentando su complejidad, caeremos en el sobreajuste (overfitting) del modelo, ajustándolo en demasía a los datos, enseñándole unas características muy concretas que no podrá generalizar. En este caso, el modelo dará mejores resultados para el conjunto de entrenamiento que para el conjunto de prueba. Por el contrario, si no alcanzamos el nivel de complejidad adecuado, nos encontraremos en la zona del subajuste (underfitting), en la que no habremos ajustado lo suficiente nuestro modelo a los datos, no le habremos enseñado lo suficiente. En cualquiera de los dos casos nuestras predicciones no serán correctas.

Existen otras técnicas de evaluación de modelos como, por ejemplo, Cross-Validation, Bootstrap, el uso de los intervalos de confianza, etc.. para intentar evitar caer en la Fosa de Carkoon, nido del todopoderoso Sarlacc.

Las iremos viendo futuros posts.