¿Y qué es un perceptrón?
Cuántas veces habremos dicho u oído eso de…es que sólo tengo una neurona y no me da para más.
¿Y si fuera cierto? Bueno, algún que otro personaje público podría servirnos de ejemplo. Pero, bromas aparte, ¿qué podríamos hacer con una única neurona? Para averiguarlo, primero tendríamos que saber cómo funciona.
El modelo biológico de una neurona tiene esta pinta:
Diagrama de una neurona. Fuente Wikipedia.
Resulta que en 1943, McCulloch y Pitts desarrollaron un modelo matemático que emula el comportamiento de una neurona. En el modelo biológico, las dentrinas tienen la función de recibir impulsos. En función de esos impulsos, se transmite una señal electroquímica a otras neuronas a través del Axón y sus terminales. La neurona McCulloch-Pitts (MCP) emula este comportamiento. El modelo recibe unas entradas, que llevan unos pesos asociados que simulan la intensidad de los impulsos. El valor de dichas señales se suma y, si dicha suma supera un cierto valor umbral, se produce una salida. El umbral actúa sobre una función de activación, que decidirá entre dos valores el valor de la salida, dependiendo si la suma de las señales supera o no dicho valor umbral.
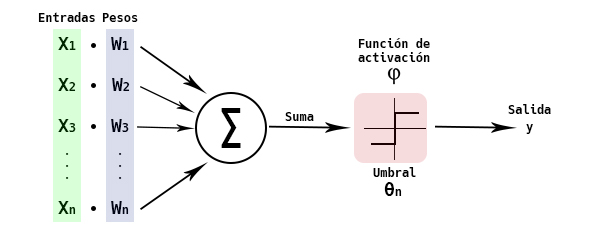
Neurona de McCulloch-Pitts
![\[ z = \sum_{i=1}^{n} x_{i}w_{i} = x_{1}w_{1} + \cdots + x_{n}w_{n} = \mathbf{w}^{T}\mathbf{x} \]](https://koldopina.com/wp-content/ql-cache/quicklatex.com-42dda4fbd4819d7bcef0f7f8c9ddbfb1_l3.png "Rendered by QuickLaTeX.com")
![\[ \varphi=\left ( z \right )\left\{ \begin{aligned} 1 \:if \:z \geqslant \theta\\ -1 \:if \:z < \theta \end{aligned} \right \quad\text{Funci\'on de activaci\'on}\]](https://koldopina.com/wp-content/ql-cache/quicklatex.com-2412a3e57947e8ad1f0b5d8f39d2ebe1_l3.png "Rendered by QuickLaTeX.com")
Haciendo una pequeña transformación podemos pasar el umbral θ al otro lado de la ecuación, lo que nos simplificará la vida. Si hacemos
![\[w_{0}=-\theta \:\:y\:\: \[x_{0}=1\]](https://koldopina.com/wp-content/ql-cache/quicklatex.com-193b14f2176d0f1589bf1f0d1d5be1a7_l3.png "Rendered by QuickLaTeX.com")
nos quedará:
![\[ z = \sum_{i=0}^{n} x_{i}w_{i} = x_{0}w_{0} + x_{1}w_{1} + \cdots + x_{n}w_{n} = \mathbf{w}^{T}\mathbf{x} \]](https://koldopina.com/wp-content/ql-cache/quicklatex.com-3ae1615611ffdf58af4d15df18540b91_l3.png "Rendered by QuickLaTeX.com")
![\[ \varphi=\left\{ \begin{aligned} 1 \:if \:z \geqslant 0\\ -1 \:if \:z < 0 \end{aligned} \right \quad\text{Funci\'on de activaci\'on}\]](https://koldopina.com/wp-content/ql-cache/quicklatex.com-c08f9b8e4c19eb502a1e2bbb49bd7ba5_l3.png "Rendered by QuickLaTeX.com")
En 1957, Frank Rosenblatt puso nombre a lo que, en Machine Learning, podríamos llamar una neurona artificial. La llamó Perceptrón. Basándose en el modelo MCP, desarrolló un algoritmo matemático que, simulando el comportamiento de las neuronas, tiene la habilidad de aprender. Lo que consigue aprender dicho algoritmo son los pesos adecuados para que la salida sea la correcta. Y como al final está decidiendo entre dos valores, podemos decir que el perceptrón está clasificando en dos clases los datos.
¿En qué consiste el algoritmo de Rosenblatt? Al perceptrón se le pasa un conjunto de datos de entrenamiento. La regla de aprendizaje del perceptrón consiste en ir añadiendo un incremento a los pesos de las entradas hasta que las salidas obtenidas por el perceptrón coincidan con las salidas esperadas del conjunto de datos de entrenamiento. Prueba y error.
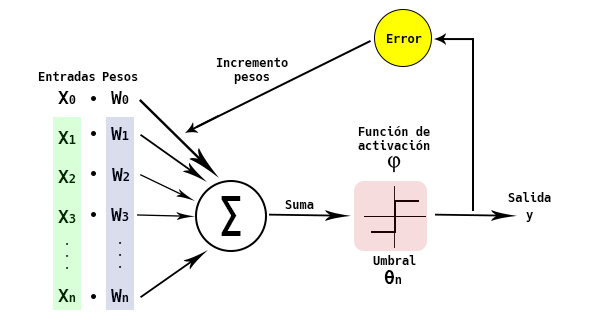
Perceptron de Frank Rosenblatt
Al comienzo del algoritmo se escoge un valor igual a cero para todos los pesos.
A continuación, para todas entradas del conjunto de datos, se calcula la salida de la neurona y se incrementan los pesos. El incremento de los pesos se calcularía así:
![\[ \Delta w_{n} = \eta( \delta_{n} - y_{n})x_{n} \]](https://koldopina.com/wp-content/ql-cache/quicklatex.com-11d55c4f6c721b01214f014bf90ee2a9_l3.png "Rendered by QuickLaTeX.com")
donde
- δ sería la salida esperada del conjunto de datos de entrenamiento
- y sería la salida calculada por la neurona.
- η sería la tasa de aprendizaje, con un valor entre 0 y 1.
Ojo!, que hay un par de peros a la hora de usar el perceptrón si queremos que converja, es decir, que logre calcular los pesos correctos y las salidas calculadas por la neurona coincidan con las salidas esperadas:
1.- El conjunto de datos tiene que ser linealmente separable.
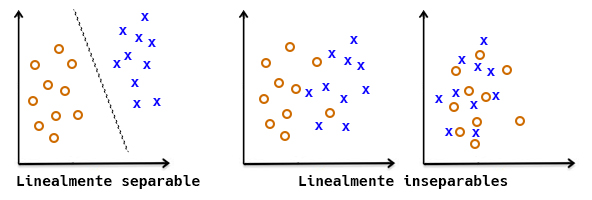2.- La tasa de aprendizaje tiene que ser suficientemente pequeña.
Si no se cumplen las dos condiciones anteriores, nuestro perceptrón seguirá intentando calcular los pesos correctos hasta el infinito, y más allá.
Bueno, hasta aquí la teoría. Ahora vamos a meternos en harina e intentar programar en Python un perceptrón que nos clasifique un conjunto de datos. Me ha sido difícil encontrar un dataset linealmente separable que no sea el típico Iris. Así que nos vamos a construir uno nosotros. Usaremos la librería de machine learning de Python: scikit-learn. Y más concretamente la función make_blobs, para generar datos aleatorios para clasificación.
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from datetime import datetime
X, y = make_blobs(n_samples=1000,n_features=2, centers=2, cluster_std=1.5)
dictdata = dict(feature1=X[:,0], feature2=X[:,1], type=y)
df = pd.DataFrame(dictdata)
now = datetime.now()
filename = 'perceptron_data_%d%d%d.csv' %(now.year, now.month, now.day)
df.to_csv(filename, sep = ';', index = False, encoding = 'utf-8')
plt.title("Random data with 'make_blobs'", fontsize='small')
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y, alpha=0.5, edgecolor='c')
plt.show()
Con éste código generamos un dataset con 1000 muestras, dos características y dos clusters, con una desviación típica de los clusters de 1.5. El código te hace una gráfica del dataset, donde se puede comprobar si son linealmente independientes. Además, guarda los datos en un archivo csv. Podéis probar hasta que el conjunto de datos devuelto por el código os convenza.
Yo he elegido un dataset que tiene esta pinta, y podéis descargar aquí.
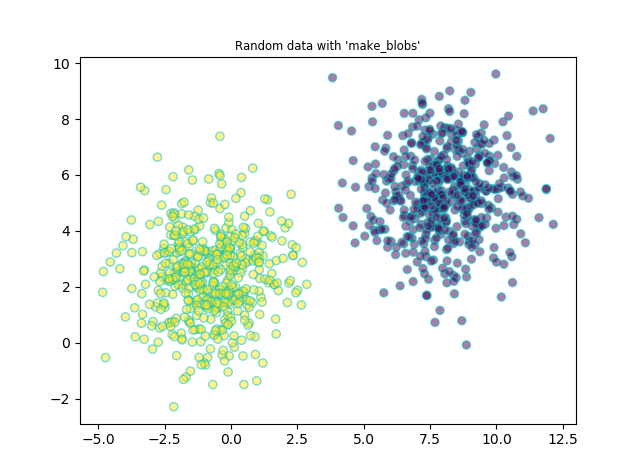
Vamos a echar un vistazo a los datos
import pandas as pd
df = pd.read_csv('perceptron_data_2018310.csv', sep=';')
print('_'*60 + 'COLUMNS')
print(df.columns.values)
print('_'*60 + 'INFO')
print (df.info())
print('_'*60 + 'DESCRIBE')
print (df.describe().transpose())
print('_'*60 + 'SHAPE')
print (df.shape)
print('_'*60 + 'COUNT VALUE CLASSES')
print (df.loc[:,'type'].value_counts())
print('_'*60 + 'NULL VALUES')
print (df.isnull().sum())
____________________________________________________________COLUMNS
['feature1' 'feature2' 'type']
____________________________________________________________INFO
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1000 entries, 0 to 999
Data columns (total 3 columns):
feature1 1000 non-null float64
feature2 1000 non-null float64
type 1000 non-null int64
dtypes: float64(2), int64(1)
memory usage: 23.5 KB
None
____________________________________________________________DESCRIBE
count mean std min 25% 50% 75% \
feature1 1000.0 3.606442 4.639656 -4.831269 -0.778176 3.339908 7.970958
feature2 1000.0 3.883439 2.126527 -2.290611 2.287451 3.816354 5.482050
type 1000.0 0.500000 0.500250 0.000000 0.000000 0.500000 1.000000
max
feature1 12.142749
feature2 9.609528
type 1.000000
____________________________________________________________SHAPE
(1000, 3)
____________________________________________________________COUNT VALUE CLASSES
1 500
0 500
Name: type, dtype: int64
____________________________________________________________NULL VALUES
feature1 0
feature2 0
type 0
dtype: int64
Ahora vamos a dividir nuestro dataset en dos conjuntos de datos, uno para el entrenamiento del perceptrón y otro para comprobar su correcto funcionamiento, con la función train_test_split.
from sklearn.model_selection import train_test_split X, y = df.loc[:, ['feature1', 'feature2']].values, df.loc[:,['type']].values X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.3)
Y creamos una clase perceptrón que va a incluir tres métodos:
- zeta: con el que se calculan los productos de las entradas por sus pesos.
- predict: con el que se calcula la salida de la neurona a partir de los datos devueltos por zeta y teniendo en cuenta la función de activación. En la teoría hemos utilizado una función de activación que tenía dos estados, el 1 si z era mayor o igual a uno y -1 para el resto de casos. En nuestros datos de entrenamiento tenemos dos estados, dos clases, 1 y 0. Por lo tanto nuestra función de activación devolverá un 1 si z es mayor o igual a uno y 0 en el resto de casos.
- fit: donde se producen las iteraciones sobre el conjunto de los datos, contando el número de iteraciones, el número de errores en cada iteración y se van actualizando los pesos hasta llegar a cero errores.
class SimplePerceptron():
def __init__(self, eta):
"""
:param eta: tasa de aprendizaje
"""
self.eta = eta
def zeta(self, X):
"""
Calcula el producto de las entradas por sus pesos
:param X: datos de entrenamiento con las caracteristicas. Array
"""
zeta = np.dot(1, self.weights[0]) + np.dot(X, self.weights[1:])
return zeta
def predict(self, X):
"""
Calcula la salida de la neurona teniendo en cuenta la función de activación
:param X: datos con los que predecir la salida de la neurona. Array
:return: salida de la neurona
"""
output = np.where(self.zeta(X) >= 0.0, 1, 0)
return output
def fit(self, X, y):
#Ponemos a cero los pesos
self.weights = [0] * (X.shape[1] + 1)
self.errors = []
self.iteraciones = 0
while True:
errors = 0
for features, expected in zip(X,y):
delta_weight = self.eta * (expected - self.predict(features))
self.weights[1:] += delta_weight * features
self.weights[0] += delta_weight * 1
errors += int(delta_weight != 0.0)
self.errors.append(errors)
self.iteraciones += 1
if errors == 0:
break
Vamos a probar el código. Creamos una instancia de la clase SimplePerceptron, y la entrenamos:
#Creamos una instancia de la clase sp = SimplePerceptron(eta=0.1) #Entrenamos sp.fit(X_train, y_train)
Podemos plotear las iteraciones con sus errores:
#Ploteamos las iteraciones y numero de errores
plt.plot(range(1, len(sp.errors) + 1), sp.errors, marker='o')
plt.xlabel('Iteracion')
plt.ylabel('Errores')
plt.tight_layout()
plt.show()
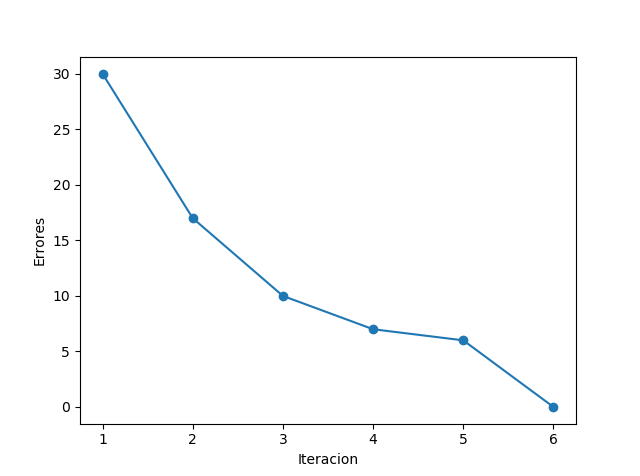
La gráfica muestra que ha necesitado 6 iteraciones sobre el conjunto de datos para calcular los pesos correctos.
Lo siguiente es pasarle a nuestro perceptrón entrenado el conjunto de datos de test y comprobar cuántos aciertos tiene:
#Comprobamos la precisión del perceptron con los datos de test
print('_'*60 + "Prediccion para X_test")
prediction = sp.predict(X_test)
print (prediction)
print('_'*60 + "Esperado para X_test")
print (y_test.T[0])
print('_'*60 + "¿Coincide lo esperado y lo devuelto por el perceptron?")
print (np.array_equal(prediction, y_test.T[0]))
print('_'*60 + "PRECISION")
print(str(np.sum(prediction == y_test.T[0])/prediction.shape[0] * 100) + ' %')
____________________________________________________________Prediccion para X_test [0 0 1 0 1 1 0 0 0 0 1 1 0 0 1 1 0 1 1 0 0 0 1 0 1 1 0 0 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 0 0 1 1 0 1 1 0 0 1 1 1 1 0 0 1 0 1 0 0 1 0 0 0 0 1 0 0 1 1 1 1 1 1 0 1 1 0 1 0 0 0 1 0 0 0 1 0 1 1 1 0 0 0 1 0 1 0 1 1 1 1 0 0 0 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 0 1 1 0 0 1 0 0 0 0 0 0 1 1 1 0 1 0 1 0 0 0 1 0 0 0 0 1 0 1 0 1 0 1 0 1 0 1 1 0 1 0 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 0 0 1 0 0 0 0 1 0 1 1 1 1 0 1 0 0 0 1 0 0 1 0 0 0 1 1 0 0 1 1 0 1 0 0 0 1 1 1 0 0 1 0 1 1 1 0 1 0 0 0 0 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 0 0 1 1 0 1 1 0 1 1 1 0 0 1 1 1 0 1 0 0 0 1 1 1 1 1 0 0 0 1 1 1 0 0 0 1 0 0 0 1 1 1 1] ____________________________________________________________Esperado para X_test [0 0 1 0 1 1 0 0 0 0 1 1 0 0 1 1 0 1 1 0 0 0 1 0 1 1 0 0 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 0 0 1 1 0 1 1 0 0 1 1 1 1 0 0 1 0 1 0 0 1 0 0 0 0 1 0 0 1 1 1 1 1 1 0 1 1 0 1 0 0 0 1 0 0 0 1 0 1 1 1 0 0 0 1 0 1 0 1 1 1 1 0 0 0 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 0 1 1 0 0 1 0 0 0 0 0 0 1 1 1 0 1 0 1 0 0 0 1 0 0 0 0 1 0 1 0 1 0 1 0 1 0 1 1 0 1 0 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 0 0 1 0 0 0 0 1 0 1 1 1 1 0 1 0 0 0 1 0 0 1 0 0 0 1 1 0 0 1 1 0 1 0 0 0 1 1 1 0 0 1 0 1 1 1 0 1 0 0 0 0 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 0 0 1 1 0 1 1 0 1 1 1 0 0 1 1 1 0 1 0 0 0 1 1 1 1 1 0 0 0 1 1 1 0 0 0 1 0 0 0 1 1 1 1] ____________________________________________________________¿Coincide lo esperado y lo devuelto por el perceptron? True ____________________________________________________________PRECISION 100.0 %
¡Magia!, tenemos un 100% de acierto sobre nuestros datos de test!
Te reto a que entrenes con otros datos a tu perceptrón!
Puedes descargarte el código de mi 
Bibliografía: Python Machine Learning, Sebastian Raschka.
