El Imperio necesita nuevos reclutas. Pilotos de caza TIE para ser más exactos.

Su número ha disminuido de forma preocupante. Es uno de los puestos dentro de la Marina Imperial que registra una mayor tasa de mortalidad.

Así que el tío Darth ha abierto un proceso de reclutamiento.

Se han presentado tropecientos n mil voluntarios en los distintos puntos de reclutamiento que el Imperio tiene a lo largo y ancho de la galaxia.

Las pruebas para entrar en la academia de vuelo son bastante duras. Y aún superándolas, no garantizan convertirse en piloto.

Una vez dentro de la academia, los reclutas se enfrentan a 6 años de formación. No todos los novatos terminan con éxito el proceso, el más exigente dentro de la Marina Imperial.

Formar un piloto le cuesta a la Marina un auténtico pastizal. Por eso quiere ajustar el tiro. Le interesa algún sistema para que se descarte a los que, aún habiendo superado las pruebas de reclutamiento, tengan mayor probabilidad de NO superar los 6 años de formación en la academia.

Y aquí entramos nosotros, porque lo valemos, y porque en post anteriores acabamos de ver un algoritmo de Machine Learning que nos viene que al pelo: la regresión logística. Éste modelo nos va a clasificar a los reclutas aspirantes a entrar en la academia que con mayor probabilidad se convertirán finalmente en pilotos de caza.

Cómo vamos con prisa, ya sabéis que el tío Darth no es conocido por su paciencia, vamos a utilizar el modelo de scikit-learn y explicar un poquito cómo ponerlo en producción para que la Marina pueda usarlo cuanto antes.

Para entrenar el modelo, se nos facilitan datos de los anteriores procesos, en los que figuran las notas obtenidas por los reclutas y una variable que nos dice si el recluta superó los 6 años de adiestramiento o si finalmente fue expulsado de la academia de vuelo.

Os lo podéis bajar de aquí.

Vamos a ver los campos que componen el dataset.

df.columns
Index(['nombre', 'planeta', 'especie', 'test_1', 'test_2', 'test_3', 'test_4', 'test_5', 'test_6', 'test_7', 'test_8', 'test_9', 'test_10', 'second_try', 'outcome'], dtype='object')

Vemos que en total se les realizaron 10 test. Además de los campos con los valores de dichos tests, se incluyen algunos datos de los aspirantes, y una columna llamada second_try, que indica si era la primera vez que el aspirante se presentaba a las pruebas o por el contrario se había presentado más veces. Su primera vez corresponde al valor cero, y el resto de valores indican el número de veces que lo intentó. El campo outcome indica si el aspirante logró terminar con éxito el curso de 6 años de la academia y finalmente convertirse en piloto de caza.

Podemos ver que en la base de datos del Imperio se guardan los resultados de las pruebas de 1.906.714 aspirantes.

df.shape

(1906714, 15)

Vamos a sacar una muestra para ver qué pinta tienen los datos.

	nombre	planeta	especie	test_1	test_2	test_3	test_4	test_5	test_6	test_7	test_8	test_9	test_10	second_try	outcome
0	Bortr Luss	Uba	Ogemite	7	6	9	9	4	4	4	9	1	5	0	0
1	Tripp Afu	Anoat	Twi’lek	8	2	9	3	2	7	2	7	9	6	0	0
2	Rowan Atar	Mardona III	Twi’lek	6	4	8	9	3	9	4	6	2	9	0	1
3	Genna Zheen	Mijos	Tof	9	6	5	6	3	8	2	6	9	2	0	0
4	Rudo Varga	Chandel	Cerean	6	9	7	6	3	4	5	6	6	8	0	1
5	Regal Kenzee	Kethmandi	Bith	6	5	4	8	9	2	7	1	5	6	0	0
6	Lyzo Bokete	Vendaxa	Terentatek	9	7	4	7	1	7	7	8	8	3	0	0
7	Spike Verbeke	Dinzo	Troig	5	6	5	7	8	6	7	3	8	7	0	0
8	Voda Bujold	Trogan	Selonian	5	9	2	8	9	8	8	8	8	1	0	0
9	Kel Wooro	Empress Teta	P’w’eck	7	9	8	6	4	6	1	5	4	2	0	0
10	Nik Tallav	Farana	Trianii	7	6	9	2	2	7	5	3	4	9	0	1
11	Karreal Khel	Woostri	Coway	6	3	4	8	5	5	1	7	3	2	0	0
12	Mathius Samlon	Dinwa Prime	Selkath	8	9	6	2	4	1	5	8	9	9	0	1
13	Aurine Lockheart	Candovant	Thakwaash	3	1	7	4	9	3	2	9	1	9	0	0
14	Zon Lee	Dagobah	Kubaz	9	7	5	3	7	8	7	7	3	7	0	1
15	Spike Cvetkovic	Lola Sayu	Chalactan	4	6	5	8	6	5	5	1	6	8	0	0
16	Tootu Nwython	Xala	Yuuzhan Vong	9	3	4	2	4	8	2	6	1	1	0	0
17	Arten Keepsala	Zeltros	Yevetha	3	5	6	2	5	3	3	1	7	1	0	0
18	Nuray Zorabos	Plexis	Whiphid	5	1	7	5	6	4	3	2	4	1	0	0
19	Riczo Richardson	Trasse	Teek	2	1	4	4	3	4	5	9	3	7	0	0

Podemos sacar una gráfica para ver cuántos aspirantes consiguieron convertirse en pilotos y cuántos no.

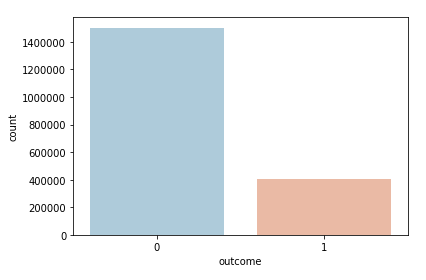
df['outcome'].value_counts()

0    1502740
1     403974
Name: outcome, dtype: int64

Vemos que solo un 21.18% de los aspirantes logró convertirse en piloto.

Por curiosidad podemos sacar el top 5 y el bottom 5 de los planetas y razas de los aspirantes de superan el curso y de los que no, respectivamente.

df[['planeta', 'outcome']].groupby('planeta').sum().sort_values(by=['outcome'], ascending=False).head(5)

TOP 5 POR PLANETAS

planeta	outcome
Botajef	2472
Ahakista	2408
Delphon	2400
Birren	2393
Byss	969

df[['planeta', 'outcome']].groupby('planeta').sum().sort_values(by=['outcome'], ascending=False).tail(5)

BOTTOM 5 POR PLANETAS

planeta	outcome
Polmanar	433
Insk	432
Mugaar	428
Dennogra	426
Vallt	421

df[['especie', 'outcome']].groupby('especie').sum().sort_values(by=['outcome'], ascending=False).head(5)

TOP 5 POR ESPECIE

especie	outcome
Gossam	1641
Gamorrean	1619
Pa’lowick	1615
Paaerduag	1608
Sauvax	1604

df[['especie', 'outcome']].groupby('especie').sum().sort_values(by=['outcome'], ascending=False).tail(5)

BOTTOM 5 POR ESPECIE

especie	outcome
Askajian	1429
Chistori	1421
Lannik	1417
Rodian	1411
Kitonak	1405

Mmm… resulta que los Gamorrean son la segunda raza que más se gradúa como piloto de caza. Bueno, es lo que tiene construirte unos datos aleatorios, la magia se rompe en algún momento…

Antes de entrenar nuestro modelo con la librería scikit-learn, vamos a utilizar otra librería de python, statmodels para crear un primer modelo de regresión logística y obtener los p-valores de las variables predictoras.

Los p-valores corresponden a los contrastes de hipótesis de cada una de las variables predictoras., y nos indican el grado de importancia en el modelo. Cuanto más grande es dicho valor, la influencia en el modelo que tiene dicha variable es más pequeña, y viceversa, cuanto más pequeño sea el p-valor, mucha más importancia tendrá en el modelo la variable correspondiente.

Así pues, las variables más significativas tendrán los valores más pequeños.

Resumiendo, los p-valores se utilizan para determinar que términos deben de mantenerse en el modelo de regresión.

Vamos a comprobar si tenemos que liquidarnos alguna columna del dataset que no nos aporte nada, quedándonos de primeras con los campos de los tests y second_try.

import statsmodels.api as sm

#VARIABLES PREDICTORAS
cols = list(df.columns[3:-1])
X = df[cols]
#VARIABLE A PREDECIR
y = df['outcome']

logit_model = sm.Logit(y, X)

result = logit_model.fit()

result.summary2()

Model:	Logit	Pseudo R-squared:	0.168
Dependent Variable:	outcome	AIC:	1637764.9357
Date:	2019-06-16 21:01	BIC:	1637902.0056
No. Observations:	1906714	Log-Likelihood:	-8.1887e+05
Df Model:	10	LL-Null:	-9.8467e+05
Df Residuals:	1906703	LLR p-value:	0.0000
Converged:	1.0000	Scale:	1.0000
No. Iterations:	7.0000

	Coef.	Std.Err.	z	P>|z|	[0.025	0.975]
test_1	0.0205	0.0007	28.6798	0.0000	0.0191	0.0219
test_2	-0.0506	0.0007	-70.5394	0.0000	-0.0520	-0.0492
test_3	-0.1761	0.0007	-238.0421	0.0000	-0.1776	-0.1747
test_4	-0.1761	0.0007	-237.8135	0.0000	-0.1775	-0.1746
test_5	-0.1939	0.0007	-260.1273	0.0000	-0.1953	-0.1924
test_6	0.1453	0.0007	198.5343	0.0000	0.1438	0.1467
test_7	-0.0489	0.0007	-68.1188	0.0000	-0.0503	-0.0475
test_8	0.0061	0.0007	8.4858	0.0000	0.0047	0.0075
test_9	-0.2017	0.0007	-269.6376	0.0000	-0.2031	-0.2002
test_10	0.3856	0.0008	466.7192	0.0000	0.3840	0.3872
second_try	-0.5334	0.0043	-124.8368	0.0000	-0.5418	-0.5250

Bueno, como podéis ver todos los p-valores son cero. Esto es así porque, como os he dicho antes con el tema del Gamorreano, los datos los he creado de forma aleatoria y resulta que todos los campos tienen la misma relevancia. Pero es muy importante fijarte en esto cuando estemos tratando datos reales, es uno de los pasos a dar para poder ajustar bien tu modelo.

Podríamos usar esta misma librería para nuestro modelo de regresión logística. Pero hemos dicho que vamos a usar scikit-learn, así que vamos a ello:

Importamos las librerías y funciones necesarias…

from sklearn import linear_model
from sklearn.model_selection import train_test_split
from sklearn import metrics

Dividimos los datos en set de entrenamiento (70%) y set de prueba (30%)…

#VARIABLES PREDICTORAS
cols = list(df.columns[3:-1])
X = df[cols]
#VARIABLE A PREDECIR
y = df['outcome']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state = 0)

Y entrenamos el modelo…

logit_model_sk = linear_model.LogisticRegression(solver='lbfgs')
logit_model_sk.fit(X,y)



LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
                   intercept_scaling=1, l1_ratio=None, max_iter=100,
                   multi_class='warn', n_jobs=None, penalty='l2',
                   random_state=None, solver='lbfgs', tol=0.0001, verbose=0,
                   warm_start=False)

Calculamos las predicciones del modelo para los datos de test…

prediction = logit_model_sk.predict(X_test)

Podemos sacar la matriz de confusión:

metrics.confusion_matrix(y_test, prediction)



array([[450064,   1060],
       [  2645, 118246]])

Calculamos alguna métrica, que ya hemos visto en post anteriores…

metrics.accuracy_score(y_test, prediction)
0.9935228971268236

metrics.precision_score(y_test, prediction)
0.9911152833889326

metrics.recall_score(y_test, prediction)
0.9781207864936182

metrics.f1_score(y_test, prediction)
0.9845751612218304

Vemos que nuestro modelo se ajusta bastante bien a los datos.

Muy bien!. Ya tenemos nuestro modelo entrenado y hemos comprobado que funciona bastante bien haciendo su trabajo de clasificación.

¿Y ahora qué?

Pues ahora hay que sacar provecho del modelo, poniéndolo en producción.

¿Qué necesitamos?. Muy sencillo. Necesitamos los coeficientes de la ecuación de regresión que vimos en Descubriendo la regresión logística

   

Necesitamos los b_n y el término independiente a.

Sencillo, se los pedimos al modelo…

coeficientes = logit_model_sk.coef_[0].tolist()



[1.0638692083623609,
 0.7373641809108851,
 0.1381370721237855,
 0.13605304050542538,
 0.049279543208178164,
 1.6248878638411526,
 0.7431579591295562,
 0.9958638321778109,
 0.01793654409627288,
 2.804762990311059,
 -0.270819960978192]

a = logit_model_sk.intercept_



array([-49.7687682])

Una vez que tenemos los coeficientes y el término independiente, lo mejor es guardarlos en un repositorio al que se puede tener acceso, por ejemplo en una tabla en una base de datos. Vamos a suponer que utilizamos una base de datos relacional tipo MySQL, SQL Server, Oracle, etc.

Lo siguiente sería programar un procedimiento en la base de datos, tal que cuando se realice una nueva inserción con las notas de un aspirante a recluta, el procedimiento calcule la probabilidad del modelo de regresión y clasifique al recluta como apto o no apto.

El procedimiento debe calcular esto:

   

En nuestro caso quedaría así:

   

   

Por ejemplo, en Python podríamos hacer esto:

import math
import numpy as np

def probabilidad(nuevos_valores):
    p = 1/(1 + math.exp(-(a + np.dot(coeficientes, nuevos_valores))))
    return p

La función coge como argumento nuevos_valores, que serían los valores de las pruebas de un nuevo recluta, y devuelve la probabilidad de que ese recluta llegue a superar los 6 años de entrenamiento.

Nos quedaría tomar una decisión importante. Hemos dicho que el modelo devuelve una probabilidad. Tenemos que decidir qué valor utilizar como límite de esa probabilidad para considerar que un recluta es apto o no. A ese límite se le suele llamar threshold.

Ésta decisión depende de múltiples factores, dependiendo del caso de negocio para el que estemos utilizando el clasificador. Por ejemplo, si lo que queremos es obtener a cuántas personas llamar para una campaña de marketing, tendremos que tener en cuenta el tamaño y los recursos de los que disponemos en nuestro Call Center, y ajustar ese threshold.

Y ojo! Al cambiar el threshold, nuestra matriz de confusión también cambiará, por lo que tendremos que ser precavidos para evitar aumentar los errores en la calificación.

Un método que nos ayudará a elegir un buen threshold será la curva ROC, de la que hablaré en mi siguiente post.

Así, cambiamos nuestro procedimiento, en nuestro caso una función de python, para añadir ese threshold como argumento:

import math
import numpy as np

def probabilidad(threshold, nuevos_valores):
    res = 0
    p = 1/(1 + math.exp(-(a + np.dot(coeficientes, nuevos_valores))))
    
    if p >= threshold:
        res = 1
return res

Y ya tendríamos nuestro modelo en producción.

Nos vemos en el siguiente post!