Creo que es un buen momento para hacer un primer ejemplo de aprendizaje automático. Implementaremos un modelo de regresión lineal simple, el modelo más sencillo, con Python. Vamos a desarrollarlo de dos formas. La primera será, como me dijo alguien hace poco, con cincel y martillo, esto es, con python puro. La segunda será utilizando la librería scikit-learn.
El objetivo de implementar un modelo estadístico es intentar explicar el comportamiento de una variable a partir de los datos de otras variables. A la variable objeto de estudio se la denomina variable de salida o de respuesta. A las variables que nos ayudarán en el estudio se las llama variables de entrada, explicativas o predictoras.
La función de regresión más sencilla es la lineal. Y dentro de ésta, la simple. Se llama así porque sólo vamos a disponer de una variable de entrada o explicativa. Este modelo es una aproximación muy simple al aprendizaje supervisado. Con él comprobaremos si existe una relación entre la variable de entrada y la de salida, e intentaremos predecir el valor de la variable de salida en función de nuestra variable de entrada.
El modelo matemático para una regresión lineal se puede escribir así:
![\[ Y = \sum \beta_{k}X_{k} + \varepsilon_{k} \]](https://koldopina.com/wp-content/ql-cache/quicklatex.com-54392aca51c8ef1478dba447144e4d6f_l3.png "Rendered by QuickLaTeX.com")
que en nuestro caso se reduciría a:
![\[ Y = \beta_{1}X + \beta_{0} + \varepsilon \rightarrow y = a + bx + \varepsilon\]](https://koldopina.com/wp-content/ql-cache/quicklatex.com-65d649d8f403b1bcf40ec46a24888ccf_l3.png "Rendered by QuickLaTeX.com")
donde
- x : variable de entrada.
- a : término independiente (intercept). Valor de y cuando x es nulo.
- b : pendiente de la recta (slope). Cuánto crece y cuando x sufre un cambio.
- y : variable de salida.
- ε : error.
Tenemos que estimar dicha recta de regresión, o, lo que es lo mismo, estimar los coeficientes a y b. El objetivo final es encontrar una recta en la que la distancia vertical de los datos a dicha recta sea mínima. Para ello vamos a emplear el método más popular, la estimación por mínimos cuadrados. Éste método fue obra de un auténtico crack, Carl Friedrich Gauss. Consiste en calcular los parámetros a y b tales que hagan mínima la suma de los cuadrados de las distancias entre los valores observados y los valores estimados. A la diferencia entre el valor del dato y la predicción se le llama residuo.
Al final del desarrollo por mínimos cuadrados, se obtienen una expresión para cada uno de los coeficiente:
![\[ a = \overline{Y} - b\overline{X} \]](https://koldopina.com/wp-content/ql-cache/quicklatex.com-96dab3d0ec5a958c288084f583bccac5_l3.png "Rendered by QuickLaTeX.com")
![\[ b = \frac{cov(X,Y)}{var(X)}\]](https://koldopina.com/wp-content/ql-cache/quicklatex.com-7fd653324731745215ea1328379603e7_l3.png "Rendered by QuickLaTeX.com")
![\[ Y = a + bX \]](https://koldopina.com/wp-content/ql-cache/quicklatex.com-242d3c6d37fc223e39c2632a1c2471f9_l3.png "Rendered by QuickLaTeX.com")
Así que vamos a empezar a escribir nuestro código. Como siempre, lo primero son los datos. Aquí podéis descargar los datos que vamos a utilizar, un csv con datos de potencia eléctrica de climatización y temperatura exterior de una planta, durante el mes de agosto.
Cincel y martillo
1.- Importamos las librerías necesarias y obtenemos los datos
import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns import random import math import csv
Abrimos el archivo y creamos una lista para cada columna.
with open('data_LR.csv', 'r') as f:
reader = csv.reader(f, delimiter='|')
OUTDOOR_TEMP = []
ELECTRIC_POWER = []
for index, row in enumerate(reader):
if index == 0:
header = row
else:
try:
outNum = float(row[0].replace(",", "."))
except:
outNum = None
OUTDOOR_TEMP.append(outNum)
try:
elecNum = float(row[1].replace(",", "."))
except:
elecNum = None
ELECTRIC_POWER.append(elecNum)
2.- Echamos un vistazo a los datos.
Para ello, he hecho una función que devuelve un diccionario donde las claves son las columnas. Los valores de éstas columnas son otro diccionario donde las claves y los valores son los correspondientes a el número de registros, las clases de datos, el número de valores nulos, la media, la desviación típica, el máximo y el mínimo.
def info(header, data_list):
"""
:param header: lista con los encabezados de las columnas
:param data_list: lista con las listas de datos de las columnas: [lista1, lista2, etc...]
:return: diccionario de diccionarios con número de registros, tipo de dato, número de na,
media, std, min, max de cada columna.
"""
from collections import defaultdict
header = header
columns = data_list
values = defaultdict()
for index, head in enumerate(header):
aux = defaultdict()
aux['len'] = len(columns[index])
aux['clases'] = set([type(ele) for ele in columns[index]])
aux['na'] = sum(1 for ele in columns[index] if ele == None)
# media
media = sum(ele for ele in columns[index] if ele != None) / len(columns[index])
aux['media'] = media
# std
n = sum(1 for ele in columns[index] if ele != None)
std = ((1 / (n - 1)) * sum((ele - media) ** 2 for ele in columns[index] if ele != None)) ** 0.5
aux['std'] = std
# minimo
aux['min'] = min(ele for ele in columns[index] if ele != None)
# maximo
aux['max'] = max(ele for ele in columns[index] if ele != None)
values[head] = aux
return values
print('_'*60 + 'COLUMNS')
print (header)
____________________________________________________________COLUMNS ['OUTDOOR_TEMP', 'ELECTRIC_POWER']
Vamos a usar nuestra función info:
print ('_'*60 + 'INFO') print (info(header, [OUTDOOR_TEMP, ELECTRIC_POWER]))
defaultdict(None,
{'ELECTRIC_POWER': defaultdict(None,
{'clases': {NoneType, float},
'len': 1496,
'max': 391.71,
'media': 285.83182486631,
'min': 0.0,
'na': 2,
'std': 41.51823016424719}),
'OUTDOOR_TEMP': defaultdict(None,
{'clases': {float},
'len': 1496,
'max': 38.310135,
'media': 28.544429085561454,
'min': 0.0,
'na': 0,
'std': 6.364374947698145})})
El resultado nos muestra que en la columna ELECTRIC_POWER hay dos valores nulos. Los eliminamos:
#Quitamos los nas index_to_drop = [index for index, val in enumerate(ELECTRIC_POWER) if val is None] ELECTRIC_POWER = [val for index, val in enumerate(ELECTRIC_POWER) if index not in index_to_drop] OUTDOOR_TEMP = [val for index, val in enumerate(OUTDOOR_TEMP) if index not in index_to_drop]
print (info(header, [OUTDOOR_TEMP, ELECTRIC_POWER]))
defaultdict(None,
{'ELECTRIC_POWER': defaultdict(None,
{'clases': {float},
'len': 1494,
'max': 391.71,
'media': 286.21446452476556,
'min': 0.0,
'na': 0,
'std': 41.51646570695531}),
'OUTDOOR_TEMP': defaultdict(None,
{'clases': {float},
'len': 1494,
'max': 38.310135,
'media': 28.54050408902272,
'min': 0.0,
'na': 0,
'std': 6.36757237847448})})
3.- Exploramos los datos.
def visual(header, X, y):
"""
:param header: Lista con los nombres de los encabezados
:param X: Lista con los valores de la columna a colocar en el eje X
:param y: Lista con los valores de la columna a colocar en el eje y
:return: matplotlib figure plot
"""
fs = 10 # fontsize
fig, axs = plt.subplots(3, 2, figsize=(6, 6))
plt.subplots_adjust(top=0.9, bottom=0.1, hspace=0.5, wspace=0.2, left=0.125, right=0.9)
axs[0, 0].scatter(X, y, c='r', edgecolors=(0, 0, 0), alpha=0.2)
axs[0, 0].set_title('Scatter %s vs %s' %(header[1], header[0]), fontsize=fs)
axs[1, 0].hist(X, color='red')
axs[1, 0].set_title('Hist %s' %header[0], fontsize=fs)
axs[0, 1].hist2d(X, y)
axs[0, 1].set_title('Hist 2D', fontsize=fs)
axs[1, 1].hist(y, color='blue')
axs[1, 1].set_title('Hist %s' %header[1], fontsize=fs)
axs[2, 0].boxplot(X)
axs[2, 0].set_title('Box %s' %header[0], fontsize=fs)
axs[2, 1].boxplot(y)
axs[2, 1].set_title('Box %s' %header[1], fontsize=fs)
plt.show()
#Ploteamos la gráfica visual(header, OUTDOOR_TEMP, ELECTRIC_POWER)
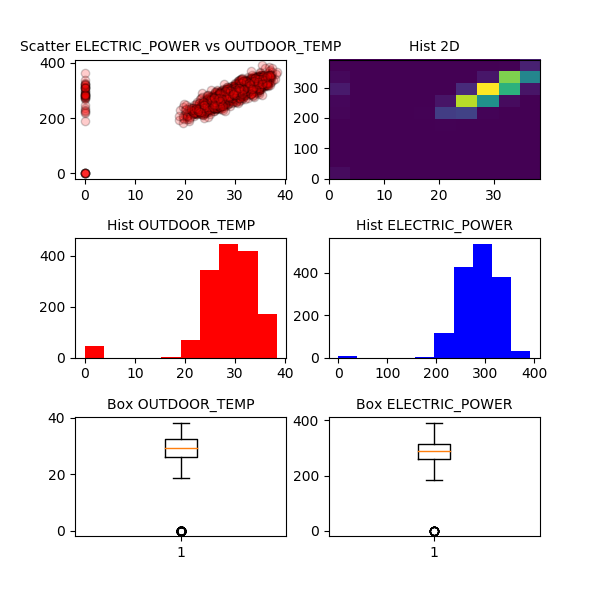En la info podemos ver que los valores mínimos en ambos campos son cero. Estos valores son atípicos (outliers), ya que la planta se encuentra en Madrid y en agosto es imposible que la temperatura baje tanto. Gráficamente queda claro que los valores cero en ambas columnas son valores atípicos. Los eliminamos.
#Quitamos los outlier o valores atípicos index_to_drop = [index for index, val in enumerate(OUTDOOR_TEMP) if val == 0] ELECTRIC_POWER = [val for index, val in enumerate(ELECTRIC_POWER) if index not in index_to_drop] OUTDOOR_TEMP = [val for index, val in enumerate(OUTDOOR_TEMP) if index not in index_to_drop]
print (info(header, [OUTDOOR_TEMP, ELECTRIC_POWER]))
defaultdict(None,
{'ELECTRIC_POWER': defaultdict(None,
{'clases': {float},
'len': 1449,
'max': 391.71,
'media': 287.81427881297435,
'min': 183.12,
'na': 0,
'std': 35.88844333632387}),
'OUTDOOR_TEMP': defaultdict(None,
{'clases': {float},
'len': 1449,
'max': 38.310135,
'media': 29.42685514768802,
'min': 18.765305,
'na': 0,
'std': 3.963016838173277})})
visual(header, OUTDOOR_TEMP, ELECTRIC_POWER)
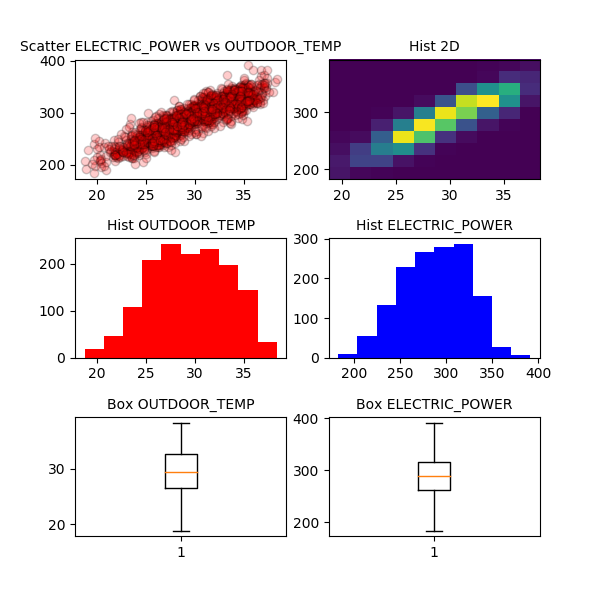
Con la gráfica de la izquierda de la primeras fila podemos aventurar que existe una relación lineal entre la temperatura exterior y la potencia de climatización de la planta.
4 .- Creamos los datos de entrenamiento y testeo.
#Creamos las listas para training y test aleatoriamente all_data = [[x_val, y_val] for x_val, y_val in zip(OUTDOOR_TEMP, ELECTRIC_POWER)] print (all_data[:5]) random.shuffle(all_data) div = math.ceil(len(all_data)*0.3) data_train = all_data[:div] data_test = all_data[div:] data_train_X = [ele[0] for ele in data_train] data_train_y = [ele[1] for ele in data_train] data_test_X = [ele[0] for ele in data_test] data_test_y = [ele[1] for ele in data_test]
5.- Creamos el modelo y lo entrenamos.
Bueno, pues ahora vamos a construir nuestro modelo. Creamos una clase que llamaremos Lin_reg.
class Lin_reg():
def __init__(self, X, Y):
"""
:param X: lista con los valores de la variable de las abscisas
:param y: lista con los valores de la variable de las ordenadas
"""
self.X = X
self.y = Y
self.N = len(self.X)
self.X_mean = sum(self.X) / len(self.X)
self.y_mean = sum(self.y) / len(self.y)
self.X_std = (1 / (self.N - 1) * sum((ele - self.X_mean) ** 2
for ele in self.X)) ** 0.5
self.y_std = (1 / (self.N - 1) * sum((ele - self.y_mean) ** 2
for ele in self.y)) ** 0.5
self.X_var = self.X_std ** 2
self.y_var = self.y_std ** 2
self.cov = sum([i * j for (i, j) in zip([ele - self.X_mean for ele in self.X],
[ele - self.y_mean for ele in self.y])]) / (self.N)
self.r = self.cov / (self.X_std * self.y_std)
def Coeficientes(self):
if len(self.X) != len(self.y):
raise ValueError('unequal length')
self.b = self.cov / self.X_var
self.a = self.y_mean - (self.b * self.X_mean)
return self.a, self.b
def predict(self, X):
yp = []
for x in X:
yp.append(self.a + self.b * x)
return yp
Creamos una instancia de la clase pasándola los datos de entrenamiento
mylinreg=Lin_reg(data_train_X,data_train_y)
y le pedimos al modelo los coeficientes de la recta de regresión
a, b = mylinreg.Coeficientes()
print('La recta de regresión es: y = %f + %f * X'%(mylinreg.Coeficientes()))
print('El coeficiente de correlación es: r = %f' %mylinreg.r)
La recta de regresión es: y = 48.043482 + 8.153666 * X El coeficiente de correlación es: r = 0.895353
Dibujamos los datos de entrenamiento y la recta de regresión:
plt.scatter(data_train_X, data_train_y, c='r', edgecolors=(0, 0, 0), alpha=0.5) plt.plot(data_train_X, [a + b * x for x in data_train_X]) plt.show()
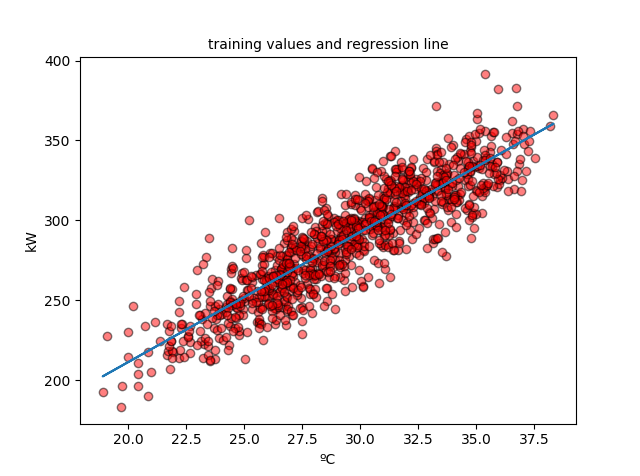
6.- Hacemos la predicción con los datos de test.
predictions = mylinreg.predict(data_test_X)
Podemos dibujar los datos de test con los datos predichos:
plt.scatter(data_test_y, predictions, c='r', edgecolors=(0, 0, 0), alpha=0.5)
plt.title('predicted values vs real values', fontsize=10)
plt.xlabel('real values')
plt.ylabel('predicted values')
plt.show()
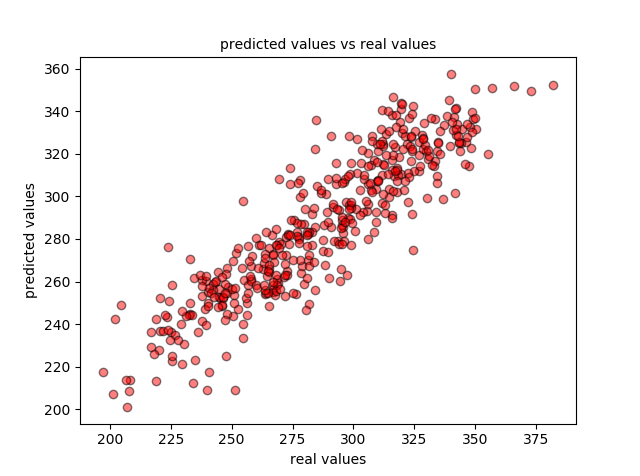
y también los datos de test con la recta de regresión:
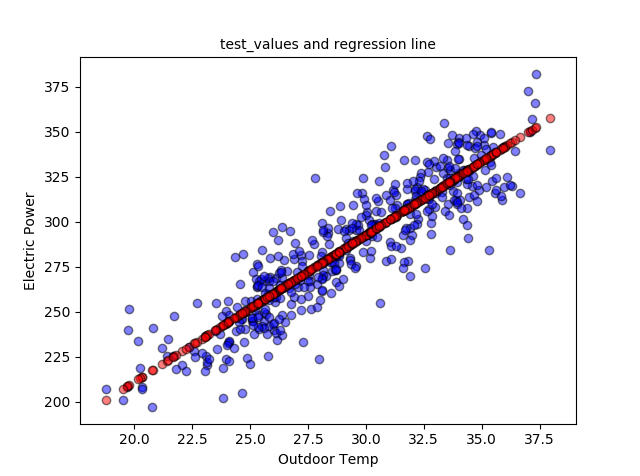
7.- Evaluación del modelo.
Para la evaluación del modelo vamos a calcular algunas métricas que luego compararemos con el modelo realizado con scikit-learn. Los indicadores de desviación que vamos a calcular son:
![\[ \begin{aligned} \underline{\textbf{Mean Error}}: ME = \frac{\sum_{i=1}^n (y - \hat{y})}{n}\\ \underline{\textbf{Mean Absolute Error}}: MAE = \frac{\sum_{i=1}^n |y - \hat{y}|}{n}\\ \underline{\textbf{Mean Square Error}}: MSE = \frac{\sum_{i=1}^n (y - \hat{y})^{2} }{n}\\ \underline{\textbf{Root Mean Square Error}}: RMSE = \sqrt{MSE}\\ \underline{\textbf{Standard Deviation of Residuals}}: SDR = \sqrt{\frac{ 1}{n-1}\sum_{i=1}^n (y - \hat{y})^{2}}\\ \end{aligned} \]](https://koldopina.com/wp-content/ql-cache/quicklatex.com-80e6dd04357cf8a90ba75257f45d60f1_l3.png "Rendered by QuickLaTeX.com")
#Metricas
#Mean Error - Desviación media
ME = sum(y_pred - y_test for y_pred, y_test in zip(predictions,data_test_y)) / len(predictions)
#Mean Absolute Error (error absoluto medio)
MAE = sum(abs(y_pred - y_test) for y_pred, y_test in zip(predictions,data_test_y)) / len(predictions)
#Mean Square Error (error cuadrático medio)
MSE = sum((y_pred - y_test)**2 for y_pred, y_test in zip(predictions, data_test_y)) / len(predictions)
#Root Mean Square Error - error de la raíz cuadrada de la media RMSE
RMSE = MSE ** 0.5
#Standard Deviation of Residuals . Desviación típica de los residuos
SDR = (1 / (len(data_test_y) - 1) * sum((y_test - y_pred) ** 2
for y_pred, y_test in zip(predictions, data_test_y))) ** 0.5
print ('Mean Error: %f' %ME)
print ('Mean Absolute Error: %f' %MAE)
print ('Mean Square Error: %f' %MSE)
print ('Root Mean Square Error: %f' %RMSE)
print ('Standard Desviation of Residuals: %f' %SDR)
Mean Error: 0.552777 Mean Absolute Error: 12.685615 Mean Square Error: 254.281254 Root Mean Square Error: 15.946199 Standard Desviation of Residuals: 15.964559
Y calculamos el coeficiente de correlación, R2, que nos dará una idea de la dependecia de las variables, al ser una medida de la relación entre ellas.
data_test_mean = sum(ele
for ele in data_test_y) / len(data_test_y)
predictions_mean = sum(ele
for ele in predictions) / len(predictions)
data_test_std = (1 / (len(data_test_y) - 1) * sum((ele - data_test_mean) ** 2
for ele in data_test_y)) ** 0.5
predictions_std = (1 / (len(predictions) - 1) * sum((ele - predictions_mean) ** 2
for ele in predictions)) ** 0.5
cov = sum([i * j
for (i, j) in zip([ele - data_test_mean
for ele in data_test_y],
[ele - predictions_mean
for ele in predictions])
]) / (len(predictions))
print('El coeficiente de correlación es: R2 = %f' % (cov * * 2 / (data_test_std * * 2 * predictions_std * * 2)))
El coeficiente de correlación es: R2 = 0.810380
Se deduce que el porcentaje de relación entre las variables que puede explicarse mediante nuestro modelo lineal es del 81,03%.
También vamos a comprobar si los errores se reparten según una distribución normal, lo que nos da una prueba de la validez de nuestro modelo.
#Distribución de los Residuos sns.distplot((np.asarray(data_test_y) - np.asarray(predictions)), bins = 50) plt.show()
python scikit-learn
1.- Importamos las librerías necesarias y obtenemos los datos que vamos a necesitar para nuestro modelo de regresión lineal simple.
import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression from sklearn import metrics import random import math
Pasamos los datos a un dataframe:
slr_df = pd.read_csv('data_LR.csv', sep="|")
slr_df = df.replace(',','.', regex=True).astype(float)
2.- Echamos un vistazo a los datos.
slr_df.head()
OUTDOOR_TEMP ELECTRIC_POWER 0 30.248541 NaN 1 31.321108 324.54 2 32.704262 NaN 3 24.938467 252.70 4 33.316906 331.10
Aquí ya vemos que tenemos dos valores NaN.
slr_df.describe()
OUTDOOR_TEMP ELECTRIC_POWER count 1496.000000 1494.000000 mean 28.544429 286.214465 std 6.364375 41.516466 min 0.000000 0.000000 25% 26.204395 261.550000 50% 29.232194 288.620000 75% 32.470816 315.852500 max 38.310135 391.710000
slr_df.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 1496 entries, 0 to 1495 Data columns (total 2 columns): OUTDOOR_TEMP 1496 non-null float64 ELECTRIC_POWER 1494 non-null float64 dtypes: float64(2) memory usage: 23.5 KB
print('_'*30 + 'NULL VALUES')
slr_df.isnull().sum()
______________________________NULL VALUES OUTDOOR_TEMP 0 ELECTRIC_POWER 2 dtype: int64
Nos cargamos los valores NaN:
slr_df = slr_df.dropna()
3.- Exploramos los datos.
Vamos a hacerlo de forma gráfica.
sns.jointplot(data = slr_df, x = 'OUTDOOR_TEMP', y ='ELECTRIC_POWER')
Eliminar los valores de temperatura exterior iguales a cero, ya que se deben a errores en la medida del sensor.
slr_df = slr_df[slr_df.OUTDOOR_TEMP != 0]
Y volvemos a dibujar
sns.jointplot(data = slr_df, x = 'OUTDOOR_TEMP', y ='ELECTRIC_POWER')
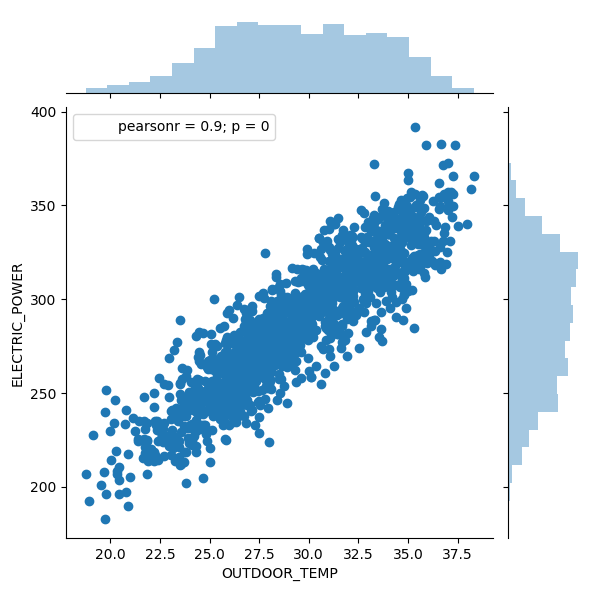
Podemos ver también la densidad de puntos.
sns.jointplot(data = slr_df, x = 'OUTDOOR_TEMP', y ='ELECTRIC_POWER', kind = 'hex')
Y dibujar un pairplot, aunque solo tengamos dos variables.
sns.pairplot(slr_df)
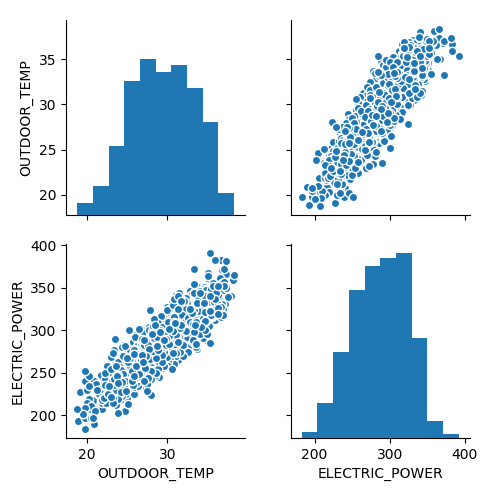
Y la nube de puntos con la recta de regresión.
sns.lmplot(data = slr_df, x = 'OUTDOOR_TEMP', y ='ELECTRIC_POWER')
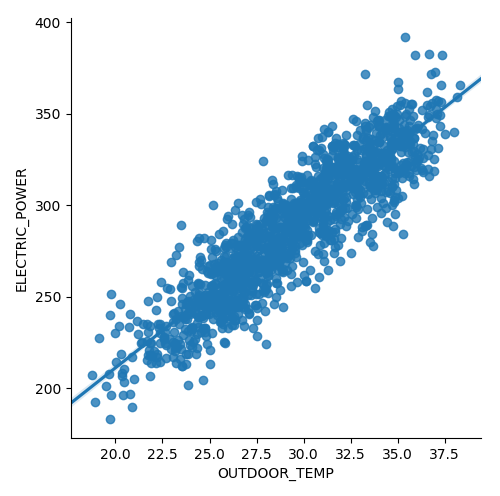
4 .- Creamos los datos de entrenamiento y testeo.
En primer lugar, creamos una variable X con los datos de la temperatura exterior, y una variable y con los datos de la potencia eléctrica.
X = slr_df['OUTDOOR_TEMP'].values.reshape(-1,1) y = slr_df['ELECTRIC_POWER'].values.reshape(-1,1)
Ahora usaremos la función train_test_split del módulo model_selection de sklearn, para crear los datos de entrenamiento y testeo. Para el tamaño de los datos de testeo elegiremos un 30% de los datos totales.
X_train, X_test, y_train, y_test = train_test_split(X, y , test_size=0.3, random_state=10)
5.- Creamos el modelo y lo entrenamos.
Usaremos el modelo LinearRegression del módulo linear_model de sklearn.
Creamos una instancia del modelo:
lm = LinearRegression()
Y lo entrenamos con los datos de entrenamiento:
lm.fit(X_train, y_train)
Le pedimos al modelo la pendiente y el término independiente de la recta:
slope = lm.coef_
intercept = lm.intercept_
print ('La recta de regresión es: y = %f + %f * X'%(lm.intercept_, slope))
La recta de regresión es: y = 48.078355 + 8.149359 * X
Prácticamente a la recta obtenida con el modelo ‘cincel y martillo’.
6.- Hacemos la predicción con los datos de test.
predictions = lm.predict(X_test)
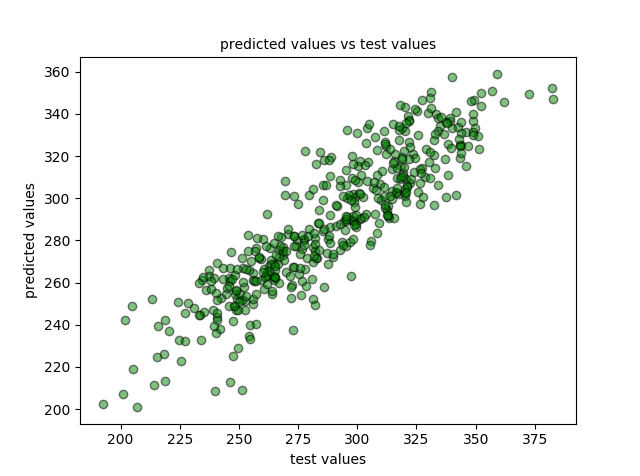
Dibujamos los datos de la predicción frente a los reales:
plt.scatter(y_test, predictions, c='g', edgecolors=(0, 0, 0), alpha=0.5)
plt.title('predicted values vs test values', fontsize=10)
plt.xlabel('test values')
plt.ylabel('predicted values')
plt.show()
7.- Evaluación del modelo.
Calculamos las mismas metricas que calculamos para nuestro modelo ‘cincel y martillo’, pero esta vez utilizando el módulo metrics de sklearn.
print('MAE: ', metrics.mean_absolute_error(y_test, predictions))
MAE: 12.731898625424554
El MAE que obtuvimos en ‘cincel’ dió: 12.685615
print('MSE: ', metrics.mean_squared_error(y_test, predictions))
MSE: 251.41283940615156
El MSE obtenido en ‘cincel’ fué: 254.28125401950533
print('RMSE: ', np.sqrt(metrics.mean_squared_error(y_test, predictions)))
RMSE: 15.856003260789006
El RMSE obtenido en ‘cincel’ fué: 15.946198732597852
print ('explained_variance_score', metrics.explained_variance_score(y_test, predictions))
print ('r2_score', metrics.r2_score(y_test, predictions)
explained_variance_score 0.8068705820651054 r2_score 0.8068238090094082
El R2 que calculamos en ‘cincel’ fué: 0.810380
Vamos a dibujar el histograma de los residuos para comprobar que tienen una distribución normal:
sns.distplot((y_test - predictions), bins = 50) plt.show()
Ambos modelos funcionan de forma similar, con unas métricas muy parecidas, y consiguen explicar alrededor de un 80% de la varianza de los datos. Sin ser una maravilla, son valores aceptables.
Puedes descargarte el código de mi 
